Integrate tan^2x by Parts

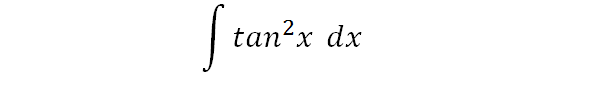
To integrate tan^2x by parts, also written as ∫tan²x dx, tan squared x, and (tan x)^2, we start by using the standard trig identity to "adjust" the integral for our needs so that we can use the standard parts formula.

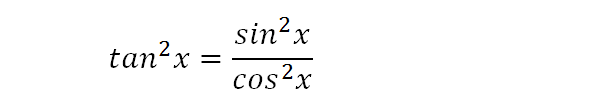
Here is a standard trig identity. Since tanx=sinx/cosx, all we have done is multiply both sides to give the above expression.

Now we adjust the expression byseperating out the sinx and introducing negative signs. It does not change anything because -sinx × -sinx = +sin²x, therefore it is the same thing.

As you can see, we now have a new integral that is the same thing, but more suited for using the integration by parts formula.

Here we refresh our minds to see what the integration by parts formula looks like. This is the standard one usually taught in schools.

We map the left hand side (LHS) of our problem to the LHS of the formula. The RHS will provide the answer, if all goes well.

As you can see, we map the term v in the formula to -sinx.

We can differentiate v with respect to (w.r.t.) dx to give a value for dv/dx. That was easy! We will keep this for later use, for substitution into the RHS of the formula.

We map (du/dx) × dx to the other half of the product in our problem.

Here, I have rewritten it so that you can see the operator d/dx more clearly. This is just to make it more clearer for my English friends.

If we integrate both sides, then the operators on the LHS cancel out. If we differentiate u w.r.t. dx, and then integrate it w.r.t. dx, then all that remains is u, because the two operators cancel each other out.

Therefore we now have an expression for u, but we are still not out of the woods yet, and there is a massive bear chasing us. We now focus on integrating the above expression using the substitution method.

Let s=cosx.

If s were to be cosx, then ds/dx=-sinx, which is a very simple differential to perform.

We now rearrange the terms to give an expression for ds.

As you can see, we can write our integral in terms of u. We replace -sinx dx with ds, and s=cosx, therefore we can now integrate s w.r.t.ds.

Just to clarify, I am rearranging it so you can see that the integral is w.r.t. ds.

Here, I rearrange it further and remove reciprocal to make it easy to see.

At this step we perform a straight integration. This is the simple one you learned first in school.

This is what it simplifies to.

We now return it into the reciprocal form as it was before, and since s=cosx, we can substitute that back in. Usually, simple steps such as these are omitted because we do them in our heads, but for the purposes of clarification they are included.

We now have an expression for u.

We now remind ourselves what all this was for by going back to the expression we first made. We take stok in knowing that we have values for u, v, and dv/dx, and all we have to do is to substitute it into the RHS of the expression above.

We found this part earlier.

We just recently found this part.

We now focus totally on the RHS of the formula since this is the side that will provide the final answer, and besides I can just about get it all on one line! Henceforth, the right hand side will be known as rhs. We substitute the values we have found to give the above expression. The multiplication sign is simply there for clarity. The negative signs cancel due to the multiplication. We also know that sinx/cosx=tanx so we substitute that into the first term. In the second term, the cosx cancels out to leave 1.

Hence the RHS simplifies to the above expression, and we only have to integrate the constant 1, which is simple to perform.

Hence this is the answer, but we put tanx into brackets, to avoid confusion, and C is the integration constant.

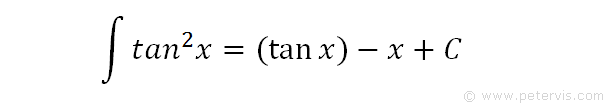
Finally, this is the solution.