Maclaurin Series for cos x

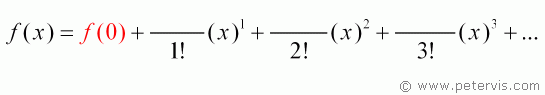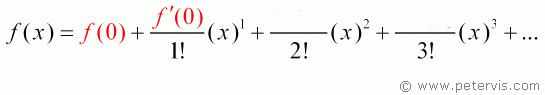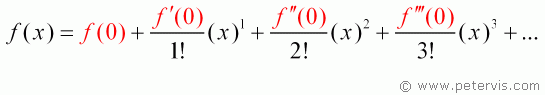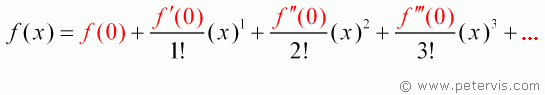
Find the Maclaurin series expansion for cos x.

This time f(x) = cos x. The first term is simply the value with x = 0, therefore cos 0 = 1.

The derivative of cos x is -sin x. When x = 0, -sin 0 = 0.

The derivative of -sin x is -cos x, and when x = 0, -cos 0 = -1

The derivative of -cos x is sin x, and when x = 0, sin 0 = 0

The derivative of sin x is cos x, and when x = 0, cos 0 = 1

As you can see there is a cyclic pattern of +1, 0, -1, 0, +1... This cyclic pattern obviously goes on infinitely but if you do not believe me then perhaps for homework, you can continue to see if there is an ending.

As you can see, I have substituted the first five terms in the top row. The next four terms in the second row are just a cyclic repetition that you can simply copy.

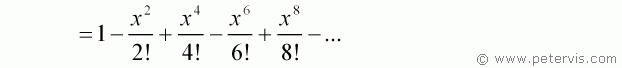
This is the Maclaurin series for cos x. It is quite amazing that a power series can represent a trigonometry function in this way. The cos x series contains even powers and factorials, and the sin x series contains odd powers and factorials. Also, notice that each successive term alternates its sign.